Konkurs matematyczny
RUSZ GŁOWĄ III tura roku szkolnego 2025/2026
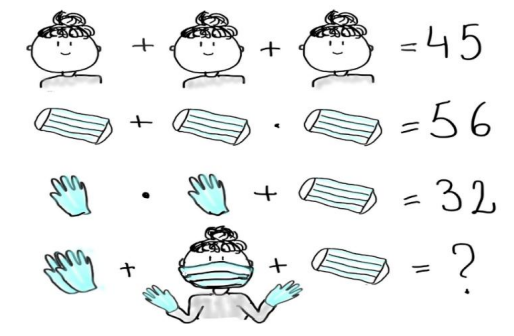
Zadanie 1.
Przyjrzyj się rysunkowi i odpowiedz, jaką wartość ma pani, maseczka i rękawiczka, a następnie oblicz wartość ostatniego równania.
Zadanie 2.
Dwa autobusy wyjechały jednocześnie naprzeciw siebie z dwóch miast A i B. Po 7 godzinach odległość między nimi wynosiła 136 km. Znajdź odległość między A i B, jeżeli pierwszy autobus może tę odległość przejechać w ciągu 12 godzin, a drugi w ciągu 10 godzin.
Zadanie 3.
Robak pełza po pniu lipy. W nocy przesuwa się o 4 metry do góry, a w dzień opuszcza się o 2 metry w dół. Ósmej nocy robak dostał się na wierzchołek drzewa. Jaka jest wysokość lipy?
Zadanie 4.
Zakatarzony Kamil używał chusteczek w kształcie kwadratu o boku 25 cm. W ciągu 8 dni zużył 3 m2 tkaniny. Ile przeciętnie zużywał chusteczek każdego dnia?
Zadanie 5.
Ogród ma kształt prostokąta, w którym długość jednego boku jest 2 razy większa od długości drugiego boku. Na mapie w skali 1:25000 obwód tego ogrodu wynosi 3,6 cm. Oblicz rzeczywiste wymiary ogrodu oraz czas potrzebny na obejście go dookoła, jeżeli piechur porusza się z prędkością 3 m/s.
Zadanie 6.
Arbuz jest o 2 kilogramy cięższy od 1/3 arbuza. Ile waży arbuz?
Pamiętaj!
Rozwiązaniem zadania są obliczenia, opis, tok rozumowania, uzasadnienie, a nie tylko podanie odpowiedzi. (regulamin konkursu – pkt 5)