Konkurs matematyczny
RUSZ GŁOWĄ IV tura roku szkolnego 2023/2024
Zadanie 1.
Bilet lotniczy z Wrocławia do Warszawy, kupowany 2 miesiące wcześniej, można kupić już nawet za 79 zł. Rodzice Jacka i Agatki, nie zdążyli zarezerwować biletów wcześniej, ale skorzystali z promocji LOTWPROMO i za bilety dla całej rodziny w jedną stronę zapłacili 265 zł. Czy kupując bilety w ofercie promocyjnej zaoszczędzili więcej niż 20%?
Zadanie 2.
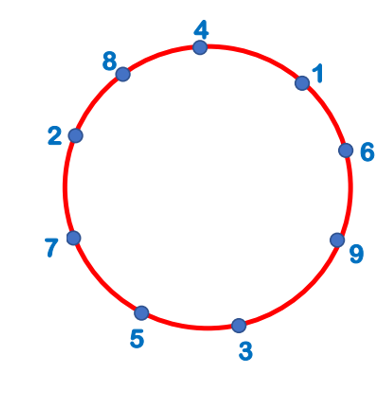
Na okręgu zaznaczono w dowolnym układzie cyfry od 1 do 9 jak na rysunku. Każde dwie kolejne cyfry odczytywane w kierunku zgodnym z kierunkiem ruchu wskazówek zegara tworzą liczbę dwucyfrową. Zapisz wszystkie utworzone liczby dwucyfrowe oraz oblicz sumę otrzymanych liczb, które są podzielne przez 3.
Zadanie 3.
Czwartoklasiści pewnej szkoły zaprojektowali kwadratową naklejkę zawierającą instrukcję Segregacji Śmieci Odpadów (patrz rysunek). Część zielona (szkło) i niebieska (papier) są takimi samymi kwadratami, każdy o obwodzie 120 cm. Pozostałe części naklejki (żółta – metale, brązowa – BIO, szara – zmieszane), to trzy jednakowe prostokąty. Jakie wymiary ma naklejka BIO?
Zadanie 4.
Wojtek przygotowując prezent dla Asi, włożył go do małego pudełka, to pudełko włożył do większego, a to do jeszcze większego, przy czym każde następne pudełko całkowicie mieściło się w poprzednim. Ustal, w jakiej kolejności brał pudełka, jeśli wiadomo, że:
1) pudełko żółte jest prostopadłościanem o objętości 12 144 cm3 i jedna z jego ścian ma wymiary 23 cm i 24 cm;
2) pudełko zielone jest sześcianem o objętości 8 000 cm3 ;
3) pudełko różowe jest sześcianem o sumie długości wszystkich krawędzi równej 312 cm.
Zadanie 5.
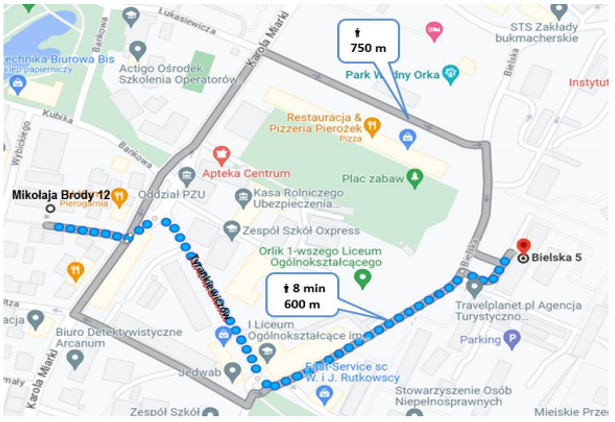
Codziennie, po odprowadzeniu brata do szkoły przy ul. Mikołaja Brody 12, Bolek idzie do szkoły przy ul. Bielskiej 5 ulicą Tyrankiewiczów obok I Liceum Ogólnokształcącego, a następnie ulicą Bielską i jest w szkole punktualnie o 8:00. Dzisiaj spóźnił się do szkoły, bo zmienił trasę – szedł ulicą Karola Miarki, następnie ulicą Łukasiewicza i ul. Bielską. O której Bolek przyszedł dzisiaj do szkoły?
Zadanie 6.
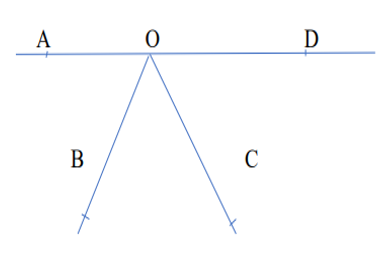
Kąt AOC ma miarę 122°, a kąt BOD ma miarę 121°. Kąty AOB, BOC, COD są kątami pewnego trójkąta. Podaj miarę najmniejszego z kątów tego trójkąta.
Pamiętaj!
Rozwiązaniem zadania są obliczenia, opis, tok rozumowania, uzasadnienie, a nie tylko podanie odpowiedzi. (regulamin konkursu – pkt 5)